Z Location Of Center Of Gravity

The location of the center of gravity The location of the center of gravity of an object determines whether it will be stable in a given position or not. The more stable an object is, the less likely it is to tip over. As long as the center of gravity is over the base of the object, it will be stable. In mathematical terms, “The center of gravity is the point at which an object’s entire mass can be assumed”. This may sound a bit abstract but with the below examples this will become clear. The CoG is not determined by shape or size, just by the weight and the location (coordinates) of each of its individual components.

Send a Note to Zig PrecChapter NextChapter Table of content
--- Under Construction ---

Z Location Of Center Of Gravity In Space

7.1 Introduction
7.2 Principle of Center of Gravity
    Concept
    Problems
7.3 Center of Gravity of 2-D bodies, centroid of areas
    Concept
    Problems
7.5 Center of Gravity, bodies of revolution
7.6 Center of Gravity, shells
7.7 Forces on submerged surfaces
7.8 Summary
7.9 Self-Test, computer programs and problems

7.1 Introduction
NextSec

In the past we determined support forces necessary to hold a bodyin equilibrium against some given external loads. In all casesthe involved forces were assumed to act on the body at given pointsand are therefore often referred to as 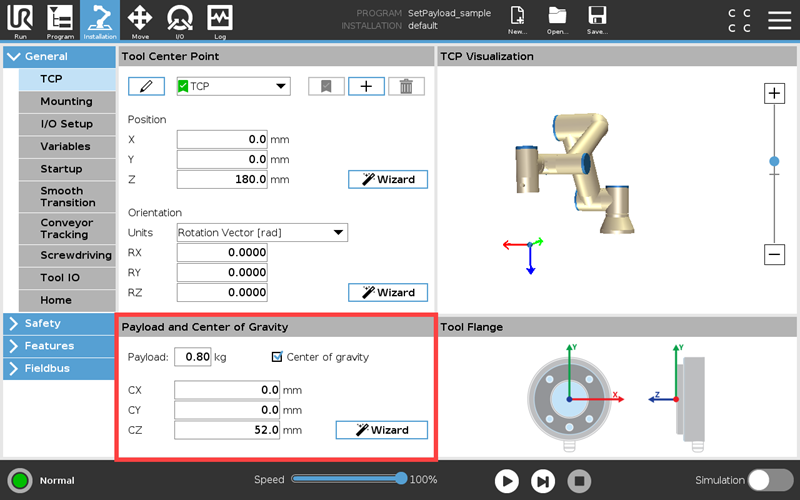Z Location Of Center Of Gravitypoint or concentrated loads.

This of course is an idealization. Even the tires of a car are in contactwith the supporting road not at a single point but over a small areawhich becomes larger when the air pressure inside the tire is low.Assuming that the force of the road onto the car is a concentrated load willreflect reality quite well as long as the size of thecontact area remains small in comparison to the distances amongthe forces involved (i.e. the distance between the wheels), which is usually the case.

In cases for which such an idealization might not lead to accurate enoughsolutions we speak of a body or structure being exposed to a continuous or distributed load. The weight(meaning the force which gravity exerts) of the structure itselfis an obvious example (although in many case the weight of thestructure might not be important in itself because it might be small in comparison to the other forces).In addition to the weight of the structure itself continuous or distributed loads come about in basically two ways :

  1. The structure we wish to investigate is in contact with another body over a finite area and has to hold up against the weight of this body. The snow load on top of a roof, a huge pile of sand on a bridge are good examples.
  2. The structure we wish to investigate is in contact with a gas or a liquid which exerts some pressure over some area.
    Water behind a dam, pressurized gas inside a container, and wind blowing against a building and the air pressure on top and underneath the wing of an airplane giving rise to the lift are good examples.

FOOT NOTE : When gravity is involved, all our calculations will be done assuming that the gravitational field is constant over the extent of the bodies we are investigating. In this case the location of the Center of Mass and the Center of Gravity of a body coincide.
For us normal earthlings this is a verygood assumption because practically all structures we are concerned withare small in comparison to the distance over which the earth's gravitationalfield changes appreciably. But the few space faring individuals among usmight get into trouble with this assumption.

TopSecTopChaptNextSec

7.2 Principle of Center of Gravity
PrecSecNextSec

Concept


Figure 7.2a
Distributed load on beam
 In Fig. 7.2a we have a simple example of a body (the triangular load) lying on top of a beam. Our goal is to determine the support forces FA and FB for a given weight W of the load and its position on the beam.

An elegant way of finding these support forces is to apply thePrinciple of the Center of Gravity. According to this principlewe replace the action of the body onto the beam by a single force equal to its weight acting at its center of gravity. (in Figure 7.2a) indicates the location of the center ofgravity, here measured as distance from the left end of the triangular load. The value of is a characteristic of the body at hand and doesnot change as the body is moved (which would change the distance 'a'in Figure 7.2a) nor does it change with the strength of the gravitational field, i.e. the location of the center of gravity isthe same on the moon as on earth.

The equilibrium equations for this case would be then

which we can solve for the two support forces.

Of course, we have to find first the location of the center of gravity(the distance in Fig. 7.2a) which depends on the way how the mass of thebody (the triangular load) is distributed.

One worry you might have when applying Equations 7.2a, is that it implies that the details of contact between the triangular loadand the beam underneath do not matter. Have a look atProblem 7.8a which investigatesthis concern.

Assuming for the moment that the location of the center of gravityof some common bodies is known, the method can be expanded to findthe support forces even if we have a composite body lying on topof our beam.

Z location of center of gravity equation

Figure 7.2b
Composite body
 Here the composite body consists of three 'elementary' or 'simple' bodies, the triangular load of weight W1, the rectangular body of weight W2, and the second triangular load of weight W3.

Again, applying the Principle of Center of Gravity, we can write downthe equilibrium equation :

which allow us to determine the two support forces uniquely.

The next question to be asked, in preparation for the next section in this chapter, is : How can we determine the location of the center of gravity of the entire composite body ? Or in other words at which location (the distance a+ in Fig. 7.2c) must I place the total weight
Wtotal = W1 + W2 + W3

of the composite body in order to obtain the same support forces as with the equations 7.2b.


Figure 7.2c
Composite body, total weight

Here is the secret as to how you can arrive at the result yourself. Write out theequilibrium equations ( sum of the forces and sum of the moments equal tozero ) for the beam of Figure 7.2c. Equate the solutionsto the results from Equat. 7.2b andafter a little bit of algebra you find :

Equation 7.2c can be used to determine the location of the center of gravity of a composite body if the locations of the center of gravitity of its individual parts with respect to a common point (here the left corner of the composite body) are known.

Equation 7.2c is more than just a prescription to determine the locationof the center of mass of a composite body. It is also the validationof the Principle of Center of Gravity : if the distance which indicates the location of the centerof gravity from the left corner of the composite body, would depend on where the composite body is located ( given by thedistance 'a' in Fig. 7.2c ) the entire concept would not makemuch sense. Right ?

Z Location Of Center Of Gravity Level

Finally, equation 7.2c can be expanded to take care of compositebodies which consist of any number, say 'n', of parts.
Mathematicians would write it this way :

meaning, that you should first add up the all the weights, Wi,of all the individual parts which are numbered 1 through n in orderto find the total weight, Wtotal.
Then proceed in summing up the moments, i Wi ,of all the individual parts with respect to a common reference point and divide by the total weight. That will give you the distance of thecenter of gravity of the composite body from the same reference point.
In my example above, the chosen reference point was the left bottom cornerof the composite body, but any other point would have been fine as well.

Problems

Prob. 7.2a : Details of Contact

TopSecTopChaptNextSec

7.3 Center of Gravity of 2-D bodies, centroid of areas
PrecSecNextSec

Concept

Using now equation 7.2d from above we want to find the centerof gravity of odd-shaped bodies subject to the following conditions(to make life a little easier) :
  1. The body has the same specific weight, , throughout. That means that each cubic inch (or whatever other measure of volume) of the body has the same weight regardless of its location inside the body.
  2. The bodies we consider have a constant thickness, t, perpendicular to the viewing plane.
Gravity

Figure 7.3a
2-D body, plate of constant thickness
 Fig. 7.3a is an example of such a body. If you like an underlying beam is represented by the x-axis. The body extends from x=a to x=b and its shape above the x-axis is assumed to be given by some mathematical function f(x). For example :

y = 3 x - 5 x2 = f(x)

for a ≤ x ≤ b and zero otherwise.

We use now the concept of composite bodies to determine the weight of sucha body and the location of its center of gravity.


Figure 7.3b
2-D body as composite body
 In Fig. 7.3b I approximate the original body by a sum of n=8 vertical strips each having the same width =(b-a)/n and the thickness t. The center of gravity of each individual strip is located at its geometric center, xi in Fig. 7.3b, halfway inbetween its left and right side. The height of each these strips is chosen to be equal to the value of f(x) at this mid-point.

The approximate weight of the composite body is now determined using Equat. 7.2d :

    (7.3a)

Here 'A' is used to denote the approximate area of the composite body.

    (7.3b)

And using Equat. 7.2d we obtain for the x-location of the center ofgravity :

    (7.3c)

Because of its constant thickness and uniform specific weight thelocation of the center of gravity, is independent of these quantities and is therefor just a property of the displayed area under the curve f(x). In thiscontext we speak of as describing thex-location of the centroid of the area under the curve f(x).

Of course the equations 7.3a through 7.3c give you only approximationsto the correct values of the area A and the location of the centroid.The quality of the approximation can be increased if the number of stripsis increased ( a short computer program may come in handy here ).In the limit of infinitely many strips of vanishingly small widthwe make the transition to integration and the above equationsbecome :

Z Location Of Center Of Gravity Equation

    (7.3d)

In Equat. 7.3d the integral over x*f(x)*dx is often referred to asthe 1. moment of the area w.r.t. the y-axis. Such quantities or propertiesof areas including the location of the centroid and higher order moments ( x2*f(x)*dx ) are of importance when discussing bending of beams (their cross-section is the area whose propertiesare of interest) on one side and in discussing the dynamic propertiesof rigd bodies on the other side. ( EMch 13 and EMch 12, respectively ).


Figure 7.3c
2-D body as composite body
We also can determine the y-location of the center of gravity byrotating Fig.3b by 90o in clockwise direction as shown inFig. 7.3c. The weight ofthe individual (now horizontal) strips is now directed parallel to the x-axisand the center of gravity of a single strip is located at a distance 1/2f(xi) away from the x-axis.

The resulting equation for the distance of the centroid (center of gravity)from the x-axis is :

    (7.3e)
Z location of center of gravity

Problems

Problem 7.3a : Area and location of centroid for f(x) = sin(x)

TopSecTopChaptNextSec

7.4 Center of Gravity, lines
PrecSecNextSec

The concept developed in this section apply to situation in which a part of a structure can be described as being slender with constant cross-section and following a particular curve.

The St. Louis Gateway Arch (if it has a constant cross-section) or themain cables of the Golden Gate Bridge in San Francisco (Diameter = 0.92 m, length = 2332m)might be some good examples but you might as well think of the cablesof a powerline leaping from tower to tower or maybe a gas pipelinegoing across mountain ranges of known profile (The center of gravitymight - admittedly - not be of interest in this case).


Figure 7.4a
Analysis of Lines
Fig. 7.4a depicts a generic example. A solid line is stretching between x=aand x=b according to some given function f(x). If this line represents somecable ( for example ) the weight of the cable iwe could determine its weightbe dividing it into small straight pieces, determine the weight of eachpiece and summing over all the pieces making up the entire cable.
The weight of such a small piece, see the insert in Fig. 7.4a, is givenby :

where A = cross-section of cable, =specific weight [g/cm3].

For all intent and purposes the small line segment is parallel to theslope f'(x) the line has at the location of the small segment which allowsus to rearrange above equation :

Adding up the contributions of all line segments gives us the totalweight :

Notice that the appearing integral contains just information about theshape of the line in terms of f'(x) and can be solved once and for allindependent of the shape and size of the cross-section and the specificweight. The integral itself merely represents the length of the line betweenthe points x=a and x=b.

TopSecTopChaptNextSec

7.5 xxxxx
PrecSecNextSec

TopSecTopChaptNextSec

7.6 xxxxxx
PrecSecNextSec

TopSecTopChaptNextSec

7.7 xxxxx
PrecSecNextSec

TopSecTopChaptNextSec

7.8 Summary
PrecSecNextSec

TopSecTopChaptNextSec

7.9 Self-Test and problems
PrecSec

Self-Test

The self-test is a multiple-choice test. It allows you to ascertain yourknowledge of the definition of terms and your understanding ofimportant results.

Sorry, none available.

Computer Programs

None available for this chapter. Sorry.

Z Location Of Center Of Gravity Defyer

Problems

Please, try them all. Some of them you might havealready done when you covered the individual sections.

Prob. 7.2a : Details of Contact
Prob. 7.3a : Area and location of centroid for f(x) = sin(x)

TopSecTopChapt

PrecChapter NextChapter Table of content

Z Location Of Center Of Gravity

Zig Herzog; hgnherzog@yahoo.com
Last revised: 10/19/09